Lijnperspectief
Onder lijnperspectief worden de verhoudingen verstaan waarop driedimensionale objecten in een plat vlak, zoals een tekening of een schilderij, zijn afgebeeld als gezien vanuit het standpunt van een waarnemer. Door de perspectivische weergave ontstaat diepte in de vlakke afbeelding. Er ontstaat een ruimtelijke indruk. Ook op een foto is lijnperspectief te herkennen. Het perspectief is afhankelijk van de plaats van de waarnemer.
Ontwikkeling
In Rome werden in het begin van de 15e eeuw klassieke bouwwerken door de beeldhouwer Filippo Brunelleschi opgemeten en vooral onderzocht op constructieve elementen en ruimtewerking. Door zijn pogingen om zijn gegevens goed op papier te krijgen ontwikkelde hij het lijnperspectief. Het werken met verdwijnpunten waar alle zichtassen samenkomen, werd door hem het eerst toegepast. Het is een goed middel om de driedimensionale ruimte op een plat oppervlak weer te geven. Hierbij waren alle afstanden meetbaar. Deze wetenschappelijke ontdekking had een enorme uitwerking op de kunsten.
De renaissanceschilder en -architect Hans Vredeman de Vries heeft veel invloed gehad op Hollandse schilders die lijnperspectief gebruikten, zoals Saenredam met zijn kerkinterieuren, en Pieter de Hooch met zijn vloertegels.
Centrale projectie op een vlak
Bij centrale projectie, met het oog als centrum, van de werkelijkheid op een verticaal projectievlak worden rechte lijnen in de werkelijkheid ook als rechte lijnen afgebeeld.
Perspectief waarbij verticale lijnen verticaal worden afgebeeld
Een van de mogelijkheden bij lijnperspectief is centrale projectie, met het oog als centrum, van de werkelijkheid op een verticaal projectievlak. Hierbij worden verticale lijnen in de werkelijkheid verticaal afgebeeld. Er is dan geen perspectief in verticale richting in de afbeelding zelf, maar eventueel wel doordat deze in een grote beeldhoek wordt bekeken, waardoor delen van de afbeelding zich verder van het oog af bevinden dan andere.
Bij deze vorm van lijnperspectief speelt de horizon vaak een grote rol. Op de horizon liggen namelijk de verdwijnpunten (ook vluchtpunten genoemd) van horizontale lijnen. In perspectief komen evenwijdige horizontale lijnen in de werkelijkheid, als ze worden doorgetrokken, bij elkaar in een verdwijnpunt op de horizon. Zo zijn in onderstaande figuur de kanten van de weg, de bovenkant en de onderkant van de gebouwen langs de weg alle evenwijdig aan elkaar. Worden hierlangs denkbeeldige lijnen getrokken, dan komen deze samen in een verdwijnpunt op de horizon.

Vaak zijn er in een afbeelding meerdere in het landschap evenwijdige lijnen in verschillende richtingen (onder een hoek van minder dan 180 graden, vaak 90 graden). Dan zijn er dus meer verdwijnpunten. In de figuur hieronder zijn er twee verdwijnpunten.

Als dit in een horizontaal vlak geplaatste rechthoekige blokken voorstelt, corresponderen de beide verdwijnpunten met horizontale kijkrichtingen die een rechte hoek met elkaar maken.
Bij een panorama-afbeelding moeten evenwijdige horizontale lijnen in de werkelijkheid waar men dwars op kijkt zowel naar links als naar rechts in de afbeelding naar elkaar toe lopen. Zulke rechte lijnen in de werkelijkheid kunnen dus niet als rechte lijnen worden afgebeeld.
Perspectief in verticale richting
Soms gebruikt een tekenaar voor de verticale evenwijdige lijnen ook een verdwijnpunt. Dit kan een sterk suggestief effect veroorzaken bij de weergave van hoge gebouwen, zoals flatgebouwen.
Analoog aan het boven opgemerkte over de weergave van evenwijdige horizontale lijnen in een panorama-afbeelding moeten evenwijdige verticale lijnen in de werkelijkheid waar men dwars op kijkt zowel naar boven als naar beneden in de afbeelding naar elkaar toe lopen. Ook zulke rechte lijnen in de werkelijkheid kunnen dus niet als rechte lijnen worden afgebeeld. Als men in de afbeelding wel rechte lijnen gebruikt kan dit alleen realistisch bij een kijkrichting recht of schuin naar boven, of recht of schuin naar beneden, niet allebei. De afbeelding hieronder is dan ook duidelijk niet realistisch voor in de werkelijkheid verticale lijnen. Het onderste deel kan alleen maar naar boven smaller wordende constructies voorstellen.
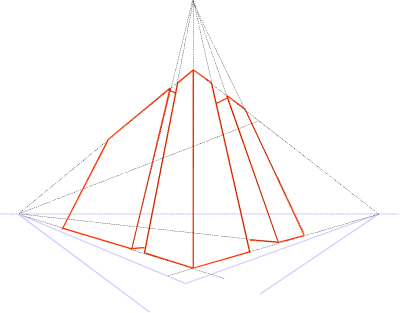
Constructie van perspectief
In een perspectivische tekening ligt het midden van bijvoorbeeld een gebouw niet midden tussen de twee muren, maar visueel gezien meer naar achter. Dit komt doordat wat verder naar voren ligt, groter lijkt. Zo lijkt de dichtstbijzijnde helft van het gebouw groter dan de achterste helft. Het midden valt te construeren door de twee diagonalen te tekenen, zoals aangegeven in de figuur hieronder.

Door deze constructie telkens te herhalen kan een rij woningen, of een weg met lichtmasten of telegraafpalen op onderling gelijke afstand, perspectivisch getekend worden. Teken eerst de voorste en de achterste telegraafpaal, en construeer de palen ertussenin.

Dubbelverhouding
De dubbelverhouding van vier punten op een lijn is invariant onder centrale projectie. Deze is dus in de afbeelding gelijk aan de waarde in werkelijkheid. Als men een getallenrechte/liniaal legt langs vier punten in de afbeelding die zich in de werkelijkheid op gelijke onderlinge afstanden op een rechte lijn bevinden, is de dubbelverhouding van de vier getalwaarden daarom gelijk aan 4. Ze zijn bijvoorbeeld 0, 6, 8, 9, met dubbelverhouding ( 8 − 0 ) ( 9 − 6 ) ( 6 − 0 ) ( 9 − 8 ) = 4 {\displaystyle {\frac {(8-0)(9-6)}{(6-0)(9-8)}}=4} . Voor drie punten in de afbeelding die zich in de werkelijkheid op gelijke onderlinge afstanden bevinden, samen met het verdwijnpunt, is de dubbelverhouding 2. In de afbeelding heeft het verdwijnpunt in het genoemde voorbeeld de getalwaarde 12, want de dubbelverhouding van 0, 6, 8, 12 is ( 8 − 0 ) ( 12 − 6 ) ( 6 − 0 ) ( 12 − 8 ) = 2 {\displaystyle {\frac {(8-0)(12-6)}{(6-0)(12-8)}}=2} , en uiteraard geeft de dubbelverhouding van 6, 8, 9, 12 hetzelfde: ( 9 − 6 ) ( 12 − 8 ) ( 8 − 6 ) ( 12 − 9 ) = 2 {\displaystyle {\frac {(9-6)(12-8)}{(8-6)(12-9)}}=2} .
Verdwijnpunten buiten het beeldvlak
In de voorbeelden hierboven waren de verdwijnpunten steeds zichtbaar. Ze kunnen echter ook buiten het beeldvlak liggen. Bij twee verdwijnpunten die corresponderen met loodrechte horizontale richtingen ligt in een afbeelding die een horizontale beeldhoek van minder dan een rechte hoek voorstelt bijvoorbeeld hoogstens één verdwijnpunt binnen het beeldvlak.
Zie ook
- Atmosferisch perspectief
- Beschrijvende meetkunde
- Gnomonische projectie
- Horizon (perspectief)
- Kleurperspectief
- Projectiemethode
- Coulissewerking
Fotogalerij
- Foto's met lijnperspectief
- De kooromgang van de Gentse Kathedraal
- Paleistuin van Caserta
- De 100 fonteinen Villa d’Este
- Evenwijdige lijnen van rails en bovenleiding
- Een rij schotelantennes van de Westerbork Synthese Radio Telescoop
- Bij deze zonnestralen ligt het verdwijnpunt bij de zon
Externe link
- Cursus perspectief door J.H. Breeschoten op kabk.nl.
 . Voor drie punten in de afbeelding die zich in de werkelijkheid op gelijke onderlinge afstanden bevinden, samen met het verdwijnpunt, is de dubbelverhouding 2. In de afbeelding heeft het verdwijnpunt in het genoemde voorbeeld de getalwaarde 12, want de dubbelverhouding van 0, 6, 8, 12 is
(
8
−
0
)
(
12
−
6
)
(
6
−
0
)
(
12
−
8
)
=
2
{\displaystyle {\frac {(8-0)(12-6)}{(6-0)(12-8)}}=2}
. Voor drie punten in de afbeelding die zich in de werkelijkheid op gelijke onderlinge afstanden bevinden, samen met het verdwijnpunt, is de dubbelverhouding 2. In de afbeelding heeft het verdwijnpunt in het genoemde voorbeeld de getalwaarde 12, want de dubbelverhouding van 0, 6, 8, 12 is
(
8
−
0
)
(
12
−
6
)
(
6
−
0
)
(
12
−
8
)
=
2
{\displaystyle {\frac {(8-0)(12-6)}{(6-0)(12-8)}}=2}
 , en uiteraard geeft de dubbelverhouding van 6, 8, 9, 12 hetzelfde:
(
9
−
6
)
(
12
−
8
)
(
8
−
6
)
(
12
−
9
)
=
2
{\displaystyle {\frac {(9-6)(12-8)}{(8-6)(12-9)}}=2}
, en uiteraard geeft de dubbelverhouding van 6, 8, 9, 12 hetzelfde:
(
9
−
6
)
(
12
−
8
)
(
8
−
6
)
(
12
−
9
)
=
2
{\displaystyle {\frac {(9-6)(12-8)}{(8-6)(12-9)}}=2}
 .
.