Standaardafwijking

Uiterlijk naar zijbalk verplaatsen verbergen

Grafiek van een normale verdeling; iedere band heeft breedte van 1 standaardafwijking.

De standaardafwijking of standaarddeviatie (vaak aangeduid met de Griekse letter σ voor de populatie en s voor de steekproef), een begrip in de statistiek, is een maat voor de spreiding van een variabele of van een verdeling of populatie. De standaardafwijking is gedefinieerd als de wortel uit de variantie, en daardoor vergelijkbaar met de waarden van de variabele zelf.

De standaardafwijking wordt gebruikt om de spreiding – de mate waarin de waarden onderling verschillen – van een verdeling aan te geven. De standaardafwijking wordt, anders dan de variantie, in dezelfde eenheid uitgedrukt als de verwachtingswaarde of het gemiddelde.

Ook voor een steekproef uit een populatie of verdeling spreekt men van standaardafwijking, of beter van steekproefstandaardafwijking, meestal aangeduid met de letter s. Deze grootheid is een schatting van de standaardafwijking in de bijbehorende populatie of verdeling. Voor een steekproef is de variantie (ongeveer) het gemiddelde van de kwadraten van de afwijking van de metingen ten opzichte van het gemiddelde van de gegevens.

Definities

Continue kansverdeling

Voor een continue kansverdeling met kansdichtheid f {\displaystyle f} $f$ is de standaardafwijking σ {\displaystyle \sigma } $\sigma$ gedefinieerd als de wortel uit de variantie, mits deze bestaat:

σ 2 = ∫ − ∞ ∞ ( x − μ ) 2 f ( x ) d x {\displaystyle \sigma ^{2}=\int _{-\infty }^{\infty }(x-\mu )^{2}f(x)\,\mathrm {d} x}

\sigma ^{2}=\int _{-\infty }^{\infty }(x-\mu )^{2}f(x)\,\mathrm {d} x

Daarin is μ {\displaystyle \mu } $\mu$ de verwachtingswaarde, gedefinieerd door:

μ = ∫ − ∞ ∞ x f ( x ) d x {\displaystyle \mu =\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x}

\mu =\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x

eveneens mits deze bestaat.

Discrete kansverdeling

Voor een discrete kansverdeling met kansfunctie p {\displaystyle p} $p$ is de standaardafwijking σ {\displaystyle \sigma } $\sigma$ analoog gedefinieerd als de wortel uit de variantie, mits deze bestaat:

σ 2 = ∑ i ( x i − μ ) 2 p ( x i ) {\displaystyle \sigma ^{2}=\sum _{i}(x_{i}-\mu )^{2}p(x_{i})}

\sigma ^{2}=\sum _{i}(x_{i}-\mu )^{2}p(x_{i})

Daarin is μ {\displaystyle \mu } $\mu$ weer de verwachtingswaarde, gedefinieerd door:

μ = ∑ i x i p ( x i ) {\displaystyle \mu =\sum _{i}x_{i}p(x_{i})}

\mu =\sum _{i}x_{i}p(x_{i})

eveneens mits deze bestaat.

Toevalsvariabele

Voor een toevalsvariabele X {\displaystyle X} $X$ met kansdichtheid f X {\displaystyle f_{X}} $f_{X}$ of kansfunctie p X {\displaystyle p_{X}} $p_{X}$ gelden dezelfde definities met respectievelijk f = f X {\displaystyle f=f_{X}} $f=f_{X}$ of p = p X {\displaystyle p=p_{X}} $p=p_{X}$ . De standaardafwijking wordt dan wel aangegeven met σ X {\displaystyle \sigma _{X}} $\sigma _{X}$ . De beide formules laten zich samenvatten in:

var ⁡ ( X ) = σ X 2 = E ⁡ ( X − μ X ) 2 {\displaystyle \operatorname {var} (X)=\sigma _{X}^{2}=\operatorname {E} (X-\mu _{X})^{2}}

\operatorname {var} (X)=\sigma _{X}^{2}=\operatorname {E} (X-\mu _{X})^{2}

waarin μ X = E ⁡ ( X ) {\displaystyle \mu _{X}=\operatorname {E} (X)} $\mu _{X}=\operatorname {E} (X)$ de verwachtingswaarde is van X {\displaystyle X} $X$ ; alles onder de voorwaarde dat de verwachtingswaarden bestaan.

De laatste formule is ook geldig voor een willekeurige toevalsvariabele.

Steekproef

Ook voor een steekproef met uitkomsten x 1 , … , x n {\displaystyle x_{1},\ldots ,x_{n}} $x_{1},\ldots ,x_{n}$ is de (steekproef)standaardafwijking gedefinieerd, meestal aangeduid met s {\displaystyle s} $s$ , als de wortel uit de (steekproef)variantie:

s 2 = 1 n − 1 ∑ i ( x i − x ¯ ) 2 {\displaystyle s^{2}={\frac {1}{n-1}}\sum _{i}(x_{i}-{\bar {x}})^{2}}

s^{2}={\frac {1}{n-1}}\sum _{i}(x_{i}-{\bar {x}})^{2}

Daarin is x ¯ = 1 n ∑ i x i {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i}x_{i}}

{\bar {x}}={\frac {1}{n}}\sum _{i}x_{i}

het steekproefgemiddelde.

En kan hiermee verder uitgewerkt worden tot een praktischere variant van de (steekproef)variantie-definitie:

s 2 = 1 n − 1 ( ∑ i x i 2 − ( ∑ i x i ) 2 n ) {\displaystyle s^{2}={\frac {1}{n-1}}\left(\sum _{i}x_{i}^{2}-{\frac {(\sum _{i}x_{i})^{2}}{n}}\right)}

s^{2}={\frac {1}{n-1}}\left(\sum _{i}x_{i}^{2}-{\frac {(\sum _{i}x_{i})^{2}}{n}}\right)

Enigszins verwarrend wordt ook de iets afwijkende grootheid

s n 2 = 1 n ∑ i ( x i − x ¯ ) 2 {\displaystyle s_{n}^{2}={\frac {1}{n}}\sum _{i}(x_{i}-{\bar {x}})^{2}}

s_{n}^{2}={\frac {1}{n}}\sum _{i}(x_{i}-{\bar {x}})^{2}

aangeduid als steekproefvariantie. (Zie Variantie#Steekproef.)

Normale verdeling

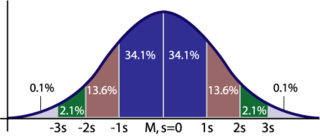
Bij normale verdelingen wijkt van de mogelijke waarden:

68,27% ten hoogste 1 keer de standaardafwijking af van de verwachtingswaarde (het midden van de verdeling)
95,45% ten hoogste 2 keer de standaardafwijking af van de verwachtingswaarde
99,73% ten hoogste 3 keer de standaardafwijking af van de verwachtingswaarde
99,9937% ten hoogste 4 keer de standaardafwijking af van de verwachtingswaarde
99,999943% ten hoogste 5 keer de standaardafwijking af van de verwachtingswaarde
99,9999998% ten hoogste 6 keer de standaardafwijking af van de verwachtingswaarde

Willekeurige verdeling

Dankzij de centrale limietstelling weten we verder dat voor veel verdelingen de verdeling van de som en dus ook van het gemiddelde van een groot aantal onafhankelijke waarnemingen daaruit, bij voldoende veel metingen bij benadering de vorm van een normale verdeling heeft. Bijgevolg gelden de bovengenoemde percentages niet alleen voor de normale verdeling, maar bij benadering ook voor het gemiddelde van een groot aantal onafhankelijke waarnemingen uit veel onbekende verdelingen.

Zie ook

Variantie

Onderwerpen uit de beschrijvende statistiek

Gemiddelden:	rekenkundig gemiddelde · meetkundig gemiddelde · harmonisch gemiddelde · kwadratisch gemiddelde · gewogen gemiddelde · getrimd gemiddelde · Winsorgemiddelde
Andere liggingsmaten:	mediaan · modus · kwartiel · deciel · percentiel
Spreidingsmaten:	variantie · standaardafwijking · variatiecoëfficiënt · interkwartielafstand
Grafische beschrijvingen:	histogram · boxplot · Q-Q plot
Overig:	moment · scheefheid · kurtosis · vijf-getallensamenvatting

Statistiek

betrouwbaarheid · centrummaat · gemiddelde · gewogen gemiddelde · interkwartielafstand · kans · kansrekening · kwartiel · mediaan · meetkundig gemiddelde · modus · p-waarde · percentiel · rekenkundig gemiddelde · schatten · significantie · scheefheid · spreiding · standaardafwijking · statistiek · statistische toets · steekproef · uitbijter · variatiecoëfficiënt · verdelingsfunctie